001什么是時間復(fù)雜度？

時間復(fù)雜度指執(zhí)行這個算法需要消耗多少時間，也可以認為是對排序數(shù)據(jù)的總的操作次數(shù)。常見的時間復(fù)雜度有：常數(shù)階O(1),對數(shù)階O(log2n),線性階O(n), 線性對數(shù)階O(nlog2n),平方階O(n2)。

//時間復(fù)雜度O(1)
sum = n*(n+1)/2; 
//時間復(fù)雜度O(n)
for(int?i = 0; i < n; i++){ 
    System.out.println("%d ",i);
} 
//時間復(fù)雜度O(n^2)
for(int?i = 0; i < n; i++){ 
    for(int?j = 0; j < n; j++){ 
        System.out.println("%d ",i); 
    }
} 
//運行次數(shù)為(1+n)*n/2//時間復(fù)雜度O(n^2)
for(int?i = 0; i < n; i++){ 
    for(int?j = i; j < n; j++){ 
        System.out.println("%d ",i); 
    }
} 
//設(shè)執(zhí)行次數(shù)為x. 2^x = n 即x = log2n,時間復(fù)雜度O(log2n)
int?i = 1, n = 100;
while(i < n){ 
    i = i * 2;
}

002常見的時間復(fù)雜度排序?

O（1）< O（logn）<O（n）<O（nlog2n）<O（n2）<O（n3）<…<O（2n）<O（n!）

003空間復(fù)雜度是什么？

空間復(fù)雜度是指算法在計算機內(nèi)執(zhí)行時所需存儲空間的度量，它也是問題規(guī)模n的函數(shù)

常見的空間復(fù)雜度有：常量空間復(fù)雜度O(1)、對數(shù)空間復(fù)雜度O(log2N)、線性空間復(fù)雜度O(n)。

004時間復(fù)雜度和空間復(fù)雜度關(guān)系？

對于一個算法來說，空間復(fù)雜度和時間復(fù)雜度往往是相互影響的。當(dāng)追求一個較好的時間復(fù)雜度時，可能會使空間復(fù)雜度的性能變差，即可能導(dǎo)致占用較多的存儲空間；反之，當(dāng)追求一個較好的空間復(fù)雜度時，可能會使時間復(fù)雜度的性能變差，即可能導(dǎo)致占用較長的運行時間。有時我們可以用空間來換取時間以達到目的。

005什么是算法穩(wěn)定性？

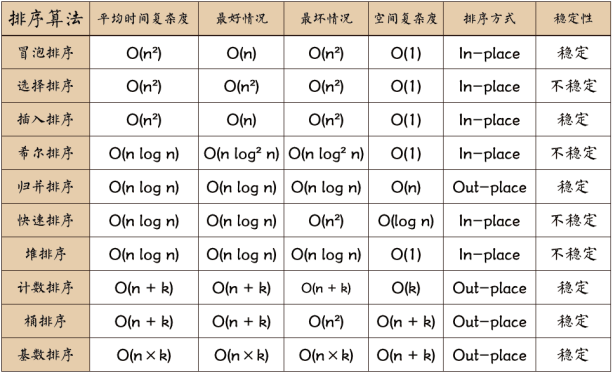
假定在待排序的記錄序列中，存在多個具有相同的關(guān)鍵字的記錄，若經(jīng)過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩(wěn)定的；否則稱為不穩(wěn)定的。排序算法是否為穩(wěn)定的是由算法具體實現(xiàn)決定的。總體上，堆排序、快速排序、希爾排序、直接選擇排序不是穩(wěn)定的排序算法，而冒泡排序、直接插入排序、歸并排序、基數(shù)排序、計數(shù)排序、桶排序是穩(wěn)定的排序算法。

006比較排序和非比較排序的區(qū)別？

比較類排序：通過比較來決定元素間的相對次序，由于其時間復(fù)雜度不能突破O(nlogn)，因此也稱為非線性時間比較類排序。如冒泡排序、選擇排序、插入排序、歸并排序、堆排序、快速排序

非比較類排序：不通過比較來決定元素間的相對次序，它可以突破基于比較排序的時間下界，以線性時間運行，因此也稱為線性時間非比較類排序。 如計數(shù)排序、基數(shù)排序、桶排序

007十大排序的復(fù)雜度及穩(wěn)定性？

008下列哪種排序算法不是穩(wěn)定的？

A. 基數(shù)排序
B. 冒泡排序
C. 選擇排序
D. 歸并排序
答案：C
解析：選擇排序是不穩(wěn)定的，如{2*，2,1}，第一次遍歷將2*與1互換，結(jié)果為{1,2,2*}，2與2*位置互換
其余排序均是穩(wěn)定的

009在各自最優(yōu)條件下,對N個數(shù)進行排序,哪個算法復(fù)雜度最低的是? （）

A. 插入排序
B. 快速排序
C. 堆排序
D. 歸并排序
答案：A
解析：插入排序：最佳O（N）
         快速排序：最佳O（NlogN）
         堆    排序：最佳O（NlogN）
         歸并排序：最佳O（NlogN），因此選擇插入排序。