![]() 二叉樹面試題
二叉樹面試題
貪心算法,看著這個名字貪心、貪婪這兩字的內在含義最為關鍵。這就好像一個貪婪的人,他事事都想要眼前看到最好的那個,看不到長遠的東西,也不為最終的結果和將來著想,貪圖眼前局部的利益最大化,有點走一步看一步的感覺。
貪心算法是尋找最優解問題的常用方法,這種方法模式一般將求解過程分成若干個步驟,但每個步驟都應用貪心原則,選取當前狀態下最好/最優的選擇(局部最有利的選擇),并以此希望最后堆疊出的結果也是最好/最優的解。
貪心算法的基本步驟:
步驟1:從某個初始解出發;
步驟2:采用迭代的過程,當可以向目標前進一步時就根據局部最優策略,得到一部分解,縮小問題規模;
步驟3:將所有解綜合起來;
假設你開了間小店,不能電子支付,錢柜里的貨幣只有 25 分、10 分、5 分和 1 分四種硬幣,如果你是售貨員且要找給客戶 41 分錢的硬幣,如何安排才能找給客人的錢既正確且硬幣的個數又最少?
這里我們需要明確的幾個點:
1.貨幣只能25分、10分、5分和1分四種硬幣;
2.找給客戶41分錢的硬幣;
3.硬幣最少化。
思考,能使用我們今天學到的貪婪算法嗎?怎么做?(回顧下貪婪算法的步驟)
1.找給顧客錢sun_money=41分錢,可選擇的是25分,10分,5分和1分四種硬幣。能找25分的就不找10分的原則,初次先找給顧客25分;
2.還差顧客sum_money=41-25=16。然后從25分、10分、5分和1分四種硬幣選取局部最優的給顧客,也就是選10分的,此時sum_money=16-10=6。重復迭代過程,還需要sum_money=6-5=1,sum_money=1-1=0。至此,顧客收到零錢,交易結束;
3.此時41分,分成1個25分,1個10分,1個5分,1個1分,總共四枚硬幣。
public static void main(String[] args){
// 不斷嘗試每種硬筆
int num25, num10, num5, num1;
num25=num10=num5=num1=0;
while(money >= 25){
num25++;
money -= 25;
}
while(money >= 10){
num10++;
money -= 10;
}
while(money >=5){
num5++;
money -=5;
}
while(money >=1){
num1++;
money -= 1;
}
System.out.println("25分有 "+num25);
System.out.println("10分有 "+num10);
System.out.println("5分有 "+num5);
System.out.println("1分有 "+num1);
return 0;
}
如何在有限的時間內有召開多個會議,要求任何兩個會議不能同時進行。
如下表是會議時間表
| 會議i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 開始時間b | 8 | 9 | 10 | 11 | 13 | 14 | 15 | 17 | 18 | 16 |
| 結束時間e | 10 | 11 | 15 | 14 | 16 | 17 | 17 | 18 | 20 | 19 |
通過會議時間表可得到比較直觀的下圖
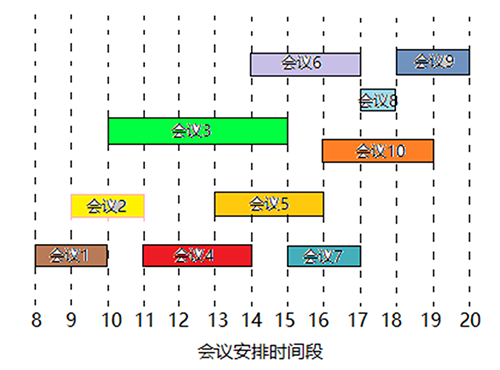
我們需要選出最多的不相交的時間段,可以嘗試以下的貪心策略:
(1)每次從剩下未安排會議中選出最早開始且與已安排會議不沖突的會議;
(2)每次從剩下未安排會議中選出持續時間最短且與已安排會議不沖突的會議;
(3)每次從剩下未安排會議中選出最早結束且與已安排會議不沖突的會議;
我們簡單地分析一下:
如果選擇最早開始時間,如果會議持續時間很長,假如8點開始,卻要持續12小時,這樣每天只能安排一個會議,肯定不合理;如果選擇持續時間最短,則可能開始時間很晚,也不合理。因此我們最好選擇開始最早而且結束時間短的會議,即最早開始時間+持續時間最短,這不就等價于選最早結束時間嘛!是不是有點兒意思~。因此,我們采用第(3)種貪心策略。
public static int bestArrange(Program[] programs, int timePoint) {
Arrays.sort(programs, new ProgramComparator());
int result = 0;
// 從左往右依次遍歷所有的會議
for (int i = 0; i < programs.length; i++) {
if (timePoint <= programs[i].start) {
result++;
timePoint = programs[i].end;
}
}
return result;
}
給你很多形如 [start, end] 的閉區間,請你設計一個算法,算出這些區間中最多有幾個互不相交的區間。舉個例子,intvs = [[1,3], [2,4], [3,6]],這些區間最多有 2 個區間互不相交,即 [[1,3], [3,6]],你的算法應該返回 2。注意邊界相同并不算相交。
思路可以分成下面三步:
1)從區間集合中選擇一個區間x,這個x是所有區間中結束最早的(end最小)。
2)把所有與x區間相交的區間從區間集合中刪除掉。
3)重復1和2,直到區間集合為空。之前選出的那些x的集合就是最大的不想交子集。

public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length == 0) {
return 0;
}
Arrays.sort(
intervals,
new Comparator < int[] > () {@
Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
//排序后的第一個必然可用
int count = 1;
int x_end = intervals[0][1];
for (int[] interval: intervals) {
if (interval[0] >= x_end) {
count++;
x_end = interval[1];
}
}
return count;
}
用貪心算法實現背包問題的求解。背包容量為20;最優解為裝入背包的物品價值總和最大。
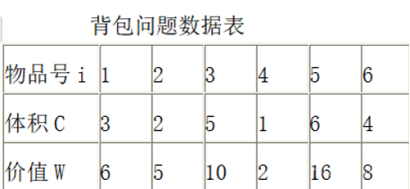
基本思想:
1)計算所有物品的性價比;
2)按物品性價比從高到低裝入,只有當高一級的性價比物品全部裝入后,才會裝入下一級的性價比物品;
3)裝到最后無法全部裝入該物品時進行部分裝入;
public class GreedyBag { // 貪心算法解決的背包問題是可以部分裝載的問題,不是0-1
static float maxV = 20; // 最大容量
float V; // 體積
float worth; // 價值
int i; // 物品編號
float cost; // 性價比,單位體積價值
static GreedyBag[] thing = new GreedyBag[6]; // 根據實際情況調整
static float[] x = new float[thing.length]; // 物品i對應的數量在下標i-1
public GreedyBag(int num, float V, float w) { // 物品信息初始化
i = num;
worth = w;
this.V = V;
cost = w / V;
thing[i - 1] = this; // 添加進數組
}
public static void sort() { // 初始化滿了再用的冒泡排序,性價比最小的沉底
float smaller; // 存儲更小的價值比
for (int i = 0; i < thing.length; i++) {
for (int j = 0; j < thing.length - i - 1; j++) {
smaller = thing[j].cost;
if (smaller < thing[j + 1].cost) { // 后面更大就交換
GreedyBag bigger = thing[j + 1];
thing[j + 1] = thing[j];
thing[j] = bigger;
}
}
}
}
public static float knapsack() {
float maxValue = 0;
float v = 0; // 已裝載體積
int i;
for (int j = 0; j < x.length; j++)
x[j] = 0; // 物品的裝載初始化為0
for (i = 0; i < thing.length; i++) {
if (v + thing[i].V > maxV)
break; // 下標i的物品沒法全部裝下
x[thing[i].i - 1] = thing[i].V; // 性價比高的全部裝下
v += thing[i].V;
maxValue += thing[i].worth;
}
if (i < thing.length) { // 由break跳出的,部分裝載
float elseV = maxV - v;
x[thing[i].i - 1] = elseV; // 部分裝載
v = maxV;
maxValue += elseV / thing[i].V * thing[i].worth;
}
return maxValue;
}
public static void printX() { // 打印裝載情況
for (int i = 0; i < x.length; i++) {
if (x[i] == 0)
continue;
System.out.println("物品編號" + (i + 1) + "裝了體積" + x[i]);
}
}
public static void main(String args[]) {
GreedyBag i1 = new GreedyBag(1, 3, 6);
GreedyBag i2 = new GreedyBag(2, 2, 5);
GreedyBag i3 = new GreedyBag(3, 5, 10);
GreedyBag i4 = new GreedyBag(4, 1, 2);
GreedyBag i5 = new GreedyBag(5, 6, 16);
GreedyBag i6 = new GreedyBag(6, 4, 8);
sort(); // 根據性價比排序
float maxValue = knapsack();
System.out.println("最大能裝價值" + maxValue + "的物品");
printX();
}
}