001什么是快速排序？

1）快排問題和荷蘭國旗問題類似，快速排序采用的思想是分治思想。主要分兩個步驟：

第一步：從要排序的數組中隨便找出一個元素作為基準(pivot),然后對數組進行分區操作,使基準左邊元素的值都不大于基準值,基準右邊的元素值都不小于基準值。

第二步就是對高段位和地段為兩部分進行遞歸排序。

2）算法圖解

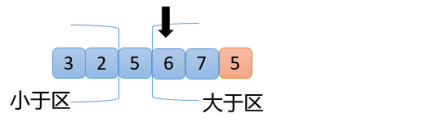
【1】從【5,3,5,6,2,7】數組中，隨機選取一個數（假設這里選的數是5）與最右邊的7進行交換 ，如下圖

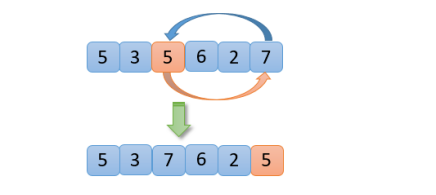
【2】準備好以5為分界點，三個區域分別為小于區、大于區（大于區包含最右側的一個數）和等于區，并準備一個指針，指向最左側的數，如下圖

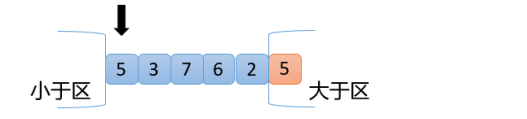
【3】接下來，每次操作都拿指針位置的數與5進行比較，交換原則如下：

-----------------------------------------------------------

原則1：指針位置的數<5

拿指針位置的數與小于區右邊第一個數進行交換

小于區向右擴大一位

指針向右移動一位

原則2：指針位置的數=5

指針向右移動一位

原則3：指針位置的數>5

拿指針位置的數與大于區左邊第一個數進行交換

大于區向左擴大一位

指針位置不動

-------------------------------------------------------

根據圖可以看出指針指向的第一個數是5，5=5，滿足交換原則2，指針向右移動一位，如下圖

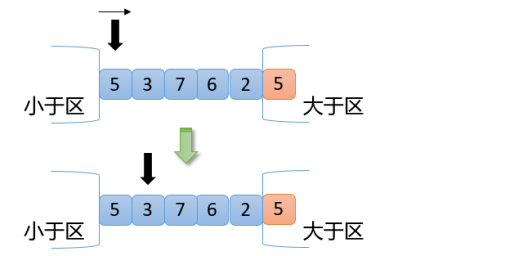
【4】從上圖可知，此時3<5，根據交換原則第1點，拿3和5（小于區右邊第一個數）交換，小于區向右擴大一位，指針向右移動一位，結果如下圖

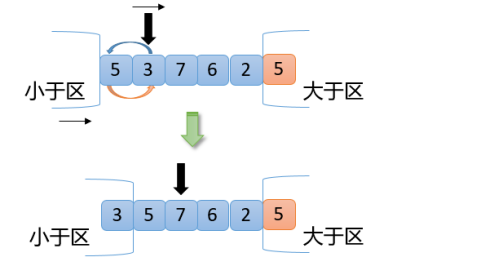
【5】從上圖可以看出，此時7>5,滿足交換原則第3點，7和2(大于區左邊第一個數)交換，大于區向左擴大一位，指針不動，如下圖

【6】從上圖可以看出，2<5,滿足交換原則第1點，2和5（小于區右邊第一個數）交換，小于區向右擴大一位，指針向右移動一位，得到如下結果

【7】從上圖可以看出，6>5，滿足交換原則第3點，6和6自己換，大于區向左擴大一位，指針位置不動，得到下面結果

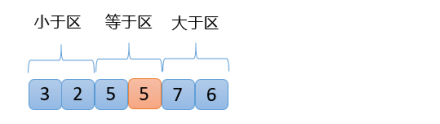
【8】此時，指針與大于區相遇，則將指針位置的數6與隨機選出來的5進行交換，就可以得到三個區域：小于區，等于區，大于區，周而復始完成最終的排序

002快速排序的代碼實現？

public static void quickSort(int[] arr) {
    if (arr == null || arr.length < 2) {
	    return;
	}
	quickSort(arr, 0, arr.length - 1);
}
// arr[l..r]排好序
public static void quickSort(int[] arr, int L, int R) {
    if (L < R) {
        swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
		int[] p = partition(arr, L, R);
		quickSort(arr, L, p[0] - 1); // < 區
		quickSort(arr, p[1] + 1, R); // > 區
	}
}
// 這是一個處理arr[l..r]的函數
// 默認以arr[r]做劃分，arr[r] -> p     <p   ==p   >p
// 返回等于區域(左邊界，右邊界), 所以返回一個長度為2的數組res, res[0] res[1]
public static int[] partition(int[] arr, int L, int R) {
    int less = L - 1; // <區右邊界
    int more = R; // >區左邊界
    int index=L;
    while (index < more) { // L表示當前數的位置   arr[R]  ->  劃分值
        if (arr[index] < arr[R]) { // 當前數   <  劃分值
            swap(arr, ++less, index++);
        } else if (arr[index] > arr[R]) { // 當前數   >  劃分值
            swap(arr, --more, index);
        } else {
            index++;
        }
    }
    swap(arr, more, R);
    return new int[] { less + 1, more };
}

003快速排序時間復雜度？

快速排序的時間復雜度在最壞情況下是O(N2)，平均的時間復雜度是O(N*lgN)。
假設被排序的數列中有N個數。遍歷一次的時間復雜度是O(N)，需要遍歷多少次呢? 至少lg(N+1)次，最多N次。 為什么最少是lg(N+1)次? 快速排序是采用的分治法進行遍歷的，我們將它看作一棵二叉樹，它需要遍歷的次數就是二叉樹的深度，而根據完全二叉樹的定義，它的深度至少是lg(N+1)。因此，快速排序的遍歷次數最少是lg(N+1)次。 為什么最多是N次? 這個應該非常簡單，還是將快速排序看作一棵二叉樹，它的深度最大是N。因此，快讀排序的遍歷次數最多是N次。

004快速排序穩定性？

快速排序是不穩定的算法，它不滿足穩定算法的定義。