![]() 二叉樹面試題
二叉樹面試題
貪心算法,看著這個名字貪心、貪婪這兩字的內在含義最為關鍵。這就好像一個貪婪的人,他事事都想要眼前看到最好的那個,看不到長遠的東西,也不為最終的結果和將來著想,貪圖眼前局部的利益最大化,有點走一步看一步的感覺。
貪心算法是尋找最優解問題的常用方法,這種方法模式一般將求解過程分成若干個步驟,但每個步驟都應用貪心原則,選取當前狀態下最好/最優的選擇(局部最有利的選擇),并以此希望最后堆疊出的結果也是最好/最優的解。
貪心算法的基本步驟:
步驟1:從某個初始解出發;
步驟2:采用迭代的過程,當可以向目標前進一步時就根據局部最優策略,得到一部分解,縮小問題規模;
步驟3:將所有解綜合起來;
假設你開了間小店,不能電子支付,錢柜里的貨幣只有 25 分、10 分、5 分和 1 分四種硬幣,如果你是售貨員且要找給客戶 41 分錢的硬幣,如何安排才能找給客人的錢既正確且硬幣的個數又最少?
這里我們需要明確的幾個點:
1.貨幣只能25分、10分、5分和1分四種硬幣;
2.找給客戶41分錢的硬幣;
3.硬幣最少化。
思考,能使用我們今天學到的貪婪算法嗎?怎么做?(回顧下貪婪算法的步驟)
1.找給顧客錢sun_money=41分錢,可選擇的是25分,10分,5分和1分四種硬幣。能找25分的就不找10分的原則,初次先找給顧客25分;
2.還差顧客sum_money=41-25=16。然后從25分、10分、5分和1分四種硬幣選取局部最優的給顧客,也就是選10分的,此時sum_money=16-10=6。重復迭代過程,還需要sum_money=6-5=1,sum_money=1-1=0。至此,顧客收到零錢,交易結束;
3.此時41分,分成1個25分,1個10分,1個5分,1個1分,總共四枚硬幣。
public static void main(String[] args){
// 不斷嘗試每種硬筆
int num25, num10, num5, num1;
num25=num10=num5=num1=0;
while(money >= 25){
num25++;
money -= 25;
}
while(money >= 10){
num10++;
money -= 10;
}
while(money >=5){
num5++;
money -=5;
}
while(money >=1){
num1++;
money -= 1;
}
System.out.println("25分有 "+num25);
System.out.println("10分有 "+num10);
System.out.println("5分有 "+num5);
System.out.println("1分有 "+num1);
return 0;
}
如何在有限的時間內有召開多個會議,要求任何兩個會議不能同時進行。
如下表是會議時間表
| 會議i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 開始時間b | 8 | 9 | 10 | 11 | 13 | 14 | 15 | 17 | 18 | 16 |
| 結束時間e | 10 | 11 | 15 | 14 | 16 | 17 | 17 | 18 | 20 | 19 |
通過會議時間表可得到比較直觀的下圖
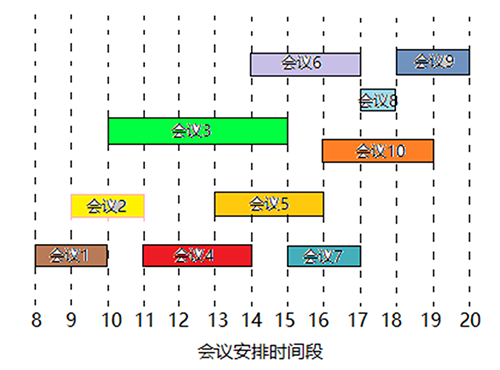
我們需要選出最多的不相交的時間段,可以嘗試以下的貪心策略:
(1)每次從剩下未安排會議中選出最早開始且與已安排會議不沖突的會議;
(2)每次從剩下未安排會議中選出持續時間最短且與已安排會議不沖突的會議;
(3)每次從剩下未安排會議中選出最早結束且與已安排會議不沖突的會議;
我們簡單地分析一下:
如果選擇最早開始時間,如果會議持續時間很長,假如8點開始,卻要持續12小時,這樣每天只能安排一個會議,肯定不合理;如果選擇持續時間最短,則可能開始時間很晚,也不合理。因此我們最好選擇開始最早而且結束時間短的會議,即最早開始時間+持續時間最短,這不就等價于選最早結束時間嘛!是不是有點兒意思~。因此,我們采用第(3)種貪心策略。
public static int bestArrange(Program[] programs, int timePoint) {
Arrays.sort(programs, new ProgramComparator());
int result = 0;
// 從左往右依次遍歷所有的會議
for (int i = 0; i < programs.length; i++) {
if (timePoint <= programs[i].start) {
result++;
timePoint = programs[i].end;
}
}
return result;
}
給你很多形如 [start, end] 的閉區間,請你設計一個算法,算出這些區間中最多有幾個互不相交的區間。舉個例子,intvs = [[1,3], [2,4], [3,6]],這些區間最多有 2 個區間互不相交,即 [[1,3], [3,6]],你的算法應該返回 2。注意邊界相同并不算相交。
思路可以分成下面三步:
1)從區間集合中選擇一個區間x,這個x是所有區間中結束最早的(end最小)。
2)把所有與x區間相交的區間從區間集合中刪除掉。
3)重復1和2,直到區間集合為空。之前選出的那些x的集合就是最大的不想交子集。

public int eraseOverlapIntervals(int[][] intervals) {
if (intervals.length == 0) {
return 0;
}
Arrays.sort(
intervals,
new Comparator < int[] > () {@
Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
//排序后的第一個必然可用
int count = 1;
int x_end = intervals[0][1];
for (int[] interval: intervals) {
if (interval[0] >= x_end) {
count++;
x_end = interval[1];
}
}
return count;
}
用貪心算法實現背包問題的求解。背包容量為20;最優解為裝入背包的物品價值總和最大。
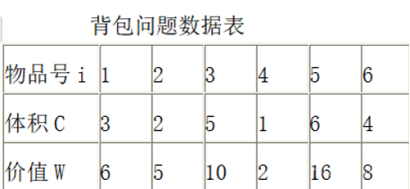
基本思想:
1)計算所有物品的性價比;
2)按物品性價比從高到低裝入,只有當高一級的性價比物品全部裝入后,才會裝入下一級的性價比物品;
3)裝到最后無法全部裝入該物品時進行部分裝入;
public class GreedyBag { // 貪心算法解決的背包問題是可以部分裝載的問題,不是0-1
static float maxV = 20; // 最大容量
float V; // 體積
float worth; // 價值
int i; // 物品編號
float cost; // 性價比,單位體積價值
static GreedyBag[] thing = new GreedyBag[6]; // 根據實際情況調整
static float[] x = new float[thing.length]; // 物品i對應的數量在下標i-1
public GreedyBag(int num, float V, float w) { // 物品信息初始化
i = num;
worth = w;
this.V = V;
cost = w / V;
thing[i - 1] = this; // 添加進數組
}
public static void sort() { // 初始化滿了再用的冒泡排序,性價比最小的沉底
float smaller; // 存儲更小的價值比
for (int i = 0; i < thing.length; i++) {
for (int j = 0; j < thing.length - i - 1; j++) {
smaller = thing[j].cost;
if (smaller < thing[j + 1].cost) { // 后面更大就交換
GreedyBag bigger = thing[j + 1];
thing[j + 1] = thing[j];
thing[j] = bigger;
}
}
}
}
public static float knapsack() {
float maxValue = 0;
float v = 0; // 已裝載體積
int i;
for (int j = 0; j < x.length; j++)
x[j] = 0; // 物品的裝載初始化為0
for (i = 0; i < thing.length; i++) {
if (v + thing[i].V > maxV)
break; // 下標i的物品沒法全部裝下
x[thing[i].i - 1] = thing[i].V; // 性價比高的全部裝下
v += thing[i].V;
maxValue += thing[i].worth;
}
if (i < thing.length) { // 由break跳出的,部分裝載
float elseV = maxV - v;
x[thing[i].i - 1] = elseV; // 部分裝載
v = maxV;
maxValue += elseV / thing[i].V * thing[i].worth;
}
return maxValue;
}
public static void printX() { // 打印裝載情況
for (int i = 0; i < x.length; i++) {
if (x[i] == 0)
continue;
System.out.println("物品編號" + (i + 1) + "裝了體積" + x[i]);
}
}
public static void main(String args[]) {
GreedyBag i1 = new GreedyBag(1, 3, 6);
GreedyBag i2 = new GreedyBag(2, 2, 5);
GreedyBag i3 = new GreedyBag(3, 5, 10);
GreedyBag i4 = new GreedyBag(4, 1, 2);
GreedyBag i5 = new GreedyBag(5, 6, 16);
GreedyBag i6 = new GreedyBag(6, 4, 8);
sort(); // 根據性價比排序
float maxValue = knapsack();
System.out.println("最大能裝價值" + maxValue + "的物品");
printX();
}
}
暴力遞歸是把問題轉化為規模縮小的同類問題的子問題 ,有明確的不需要繼續進行遞歸的條件(base case),有當得到了子問題的結果之后的決策過程并且不記錄每一個子問題的解。
相傳在古印度圣廟中,有一種被稱為漢諾塔(Hanoi)的游戲。該游戲是在一塊銅板裝置上,有三根桿(編號A、B、C),在A桿自下而上、由大到小按順序放置64個金盤。
游戲的目標:把A桿上的金盤全部移到C桿上,并仍保持原有順序疊好。
操作規則:每次只能移動一個盤子,并且在移動過程中三根桿上都始終保持大盤在下,小盤在上,操作過程中盤子可以置于A、B、C任一桿上。
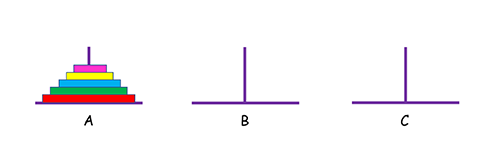
思想
假設只有一個盤子
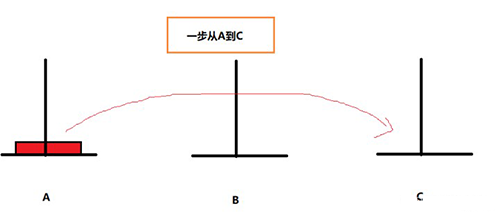
如果有兩個盤子
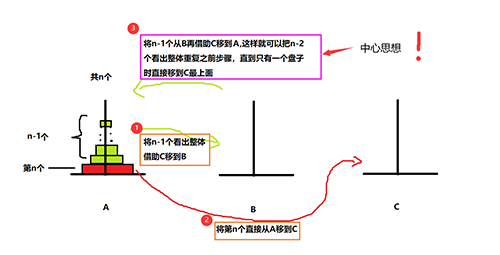
// 1~i 圓盤 目標是from -> to, other是另外一個
public static void func(int N, String from, String to, String other) {
if (N == 1) { // base
System.out.println("Move 1 from " + from + " to " + to);
} else {
func(N - 1, from, other, to);
System.out.println("Move " + N + " from " + from + " to " + to);
func(N - 1, other, to, from);
}
}
打印一個字符串的全部子序列,包括空字符串
有字符串“abc”,字符串長度為3,下標分別是0,1,2。則決策的過程一共有三個,令初始序列為空字符串。分別是:
0:此時有兩種情況,要不要'a',如果要,子序列變為“a”;如果不要則還是空字符串;
1:此時有兩種情況,要不要‘b’,加上上一步的兩種這里就有4種情況,這里不一一列舉;
2:此時有兩種情況,要不要‘c’,加上上一步的四種情況這里就有8種情況。
public class PrintAllSubsquences {
public static void pringAllSub(char[] str, int i, String res) {
if (i == str.length) {
System.out.println(res);
return;
}
//兩種情況
pringAllSub(str, i + 1, res);
pringAllSub(str, i + 1, res + str[i]);
}
public static void main(String[] args) {
String str = "abc";
pringAllSub(str.toCharArray(), 0, "");
}
}
n 皇后問題研究的是如何將 n 個皇后放置在 n×n 的棋盤上,并且使皇后彼此之間不能相互攻擊(同一行、同一列、同一斜線上的皇后都會自動攻擊)。
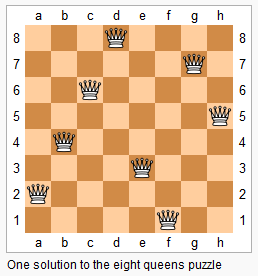
思路
1. 準備一個數組record[i],record[i] 表示 i行的皇后,放在了第幾列
2. 如果第一個皇后的在i1行j1列,第二個皇后在i1行j2列,那么應該滿足的條件是
不能共斜線:|i1-i2|不等于|j1-j2|
不能共行: i1不等于i2
不能共列:j1不等于j2
public class NQueens {
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n]; // record[i] -> i行的皇后,放在了第幾列
return process1(0, record, n);
}
// 返回值是,擺完所有的皇后,合理的擺法有多少種
public static int process1(int i, int[] record, int n) {
if (i == n) { // 終止行
return 1;
}
int res = 0;
for (int j = 0; j < n; j++) { // 當前行在i行,嘗試i行所有的列 -> j
// 當前i行的皇后,放在j列,會不會和之前(0..i-1)的皇后,不共行共列或者共斜線,
// 如果是,認為有效
// 如果不是,認為無效
if (isValid(record, i, j)) {
record[i] = j;
res += process1(i + 1, record, n);
}
}
return res;
}
// 返回i行皇后,放在了j列,是否有效
public static boolean isValid(int[] record, int i, int j) {
for (int k = 0; k < i; k++) { // 之前的某個k行的皇后
if ((j == record[k]) ||(Math.abs(record[k] - j) == Math.abs(i - k))) {
return false;
}
}
return true;
}
}
小明走樓梯,一次可以跨兩個臺階,也可以跨一個臺階,求有n個臺階,一共有多少種跨發?
從問題中我們可以分析出,如果邁上最后一個臺階,可以是一步,也可以是兩步。
分析:
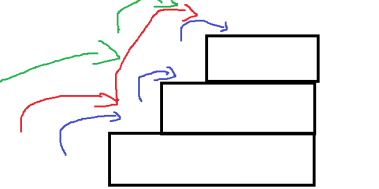
可以理解為:
f(n)=f(n-1)+f(n-2)
同理:
f(n-1)=f(n-1-1)+f(n-1-2)
f(n-2)=f(n-2-1)+f(n-2-2)
. …
…
f(4)=f(3)+f(2)
f(3)=f(2)+f(1)
f(2)=2
f(1)=1
int getNum(int n) {
if (n <= 0)return 0;
if (n == 1) return 1;
if (n == 2) return 2;
int arr = new int[n+1];
arr[1] = 1;
arr[2] = 2;
for (int i = 3; i <= n; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
int ret = arr[n];
return ret;
}
你讓工人為你工作7天,給工人的回報是一根金條。金條平分成相連的7段,你必須在每天結束時給他們一段金條,如果只許你兩次把金條弄斷,你如何給你的工人付費?
將金條分成1段、2段和4段
第?天給1段金條
第?天把1段金條要回,給2段金條
第三天給1段金條
第四天把1段和2段金條要回,給4段金條
第五天給1段金條
第六天把1段金條要回,給2段金條
第七天給1段金條
12個球和一個天平,現知道只有一個和其它的重量不同,問怎樣稱才能用三次就找到那個球? (注意此題并未說明那個球的重量是輕是重,所以需要仔細考慮)
首先,把12個小球分成三等份,每份四只。
拿出其中兩份放到天平兩側稱(第一次)
情況1:天平是平衡的。
那么那八個拿上去稱的小球都是正常的,特殊的在四個里面。
把剩下四個小球拿出三個放到一邊,另一邊放三個正常的小球(第二次)
如天平平衡,特殊的是剩下那個。
如果不平衡,在天平上面的那三個里。而且知道是重了還是輕了。
剩下三個中拿兩個來稱,因為已經知道重輕,所以就可以知道特殊的了。(第三次)
情況2:天平傾斜。
特殊的小球在天平的那八個里面。
把重的一側四個球記為A1A2A3A4,輕的記為B1B2B3B4。
剩下的確定為四個正常的記為C。
把A1B2B3B4放到一邊,B1和三個正常的C小球放一邊。(第二次)
情況2.1:天平平衡了。
特殊小球在A2A3A4里面,而且知道特殊小球比較重。
把A2A3稱一下,就知道三個里面哪個是特殊的了。(第三次)
情況2.2:天平依然是A1的那邊比較重。
特殊的小球在A1和B1之間。
隨便拿一個和正常的稱,就知道哪個特殊了。(第三次)
情況2.3:天平反過來,B1那邊比較重了。
特殊小球在B2B3B4中間,而且知道特殊小球比較輕。
把B2B3稱一下,就知道哪個是特殊的了。(第三次)
燒一根不均勻的繩,從頭燒到尾總共需要1個小時。現在有若干條材質相同的繩子,問如何用燒繩的方法來計時一個小時十五分鐘呢?
取3根繩
先將第一根的兩頭都點燃,同時將第二根的某一頭點燃。(t=0)
待第一根燒盡,點燃第二根的另一頭。(t=30min)
待第二根燒盡,點燃第三根的兩頭。(t=45min)
待第三根燒盡,t=75min。
1元錢一瓶汽水,喝完后兩個空瓶換一瓶汽水,問: 你有20元錢,最多可以喝到幾瓶汽水?
最多可以喝40瓶
首先20空瓶可以換10瓶水,10空瓶可以換5瓶水,4空瓶可以換2瓶水,2空瓶可以換1瓶水,1個空瓶加上(5-4)那個空瓶又可以換1瓶水,然后一個空瓶加借一個瓶再喝一瓶還一個瓶子。總共喝了20+10+5+2+1+1+1=40
據說有人給酒肆的老板娘出了一個難題: 此人明明知道店里只有兩個舀酒的勺子,分別能舀7兩和11兩酒,卻硬要老板娘賣給他2兩酒。聰明的老板娘毫不含糊,用這兩個勺子在酒缸里舀酒,并倒來倒去,居然量出了2兩酒,聰明的你能做到嗎?
將7裝滿,倒入11,再裝滿,倒滿11兩勺子。---》此時7兩勺子那個里面是3。
將11倒空,7中3倒入11,再裝滿7倒入11。---》此時11兩那個里面是10。
將7再次裝滿,倒滿11。---》此時7兩那個里面是6。
將11再次倒空,7中6倒入11。---》此時7兩那個里面是0,11兩里面是6兩
將7再次裝滿,倒滿11。---》此時7兩那個里面是2
桌上有100個蘋果,你和另一個人一起拿,一人一次,每次拿的數量大于等于1小于等于5,問:如何拿能保證最后一個蘋果由你來拿?
解答:只需要你先拿,第一次拿4個,以后看對方拿的個數,根據對方拿的個數,保證每輪對方和你拿的加起來是6就行了,其實就是保證你拿到4,還要拿到10,16...直到94。
請把一盒蛋糕切成8份,分給8個人,但蛋糕盒里還必須留有一份。
解答:面對這樣的怪題,有些應聘者絞盡腦汁也無法分成;而有些應聘者卻感到此題實際很簡單,把切成的8份蛋糕先拿出7份分給7人,剩下的1份連蛋糕盒一起分給第8個人。
一樓到十樓的每層電梯門口都放著一顆鉆石,鉆石大小不一。你乘坐電梯從一樓到十樓,每層樓電梯門都會打開一次,只能拿一次鉆石,問怎樣才能拿到最大的一顆?
解答:一樓門打開,拿鉆石,然后到二樓之后比較二樓和手里的鉆石,誰大拿哪個,
然后到三樓之后比較三樓和手里的鉆石,誰大拿哪個....依次類推,到十樓的時候就可以拿到最大的那個鉆石。