二叉查找樹（Binary Search Tree）又稱二叉排序樹、二叉搜索樹。二叉查找樹是為了實現快速查找而生的，一般情況下，查詢效率比鏈表結構要高。不過，它不僅僅支持快速查找一個數據，還支持快速插入、刪除一個數據。二叉查找樹要求，在樹中的任意一個節點都要滿足，其左子樹中每個節點的值，都要小于這個節點的值，而右子樹每個節點的值都大于這個節點的值。二叉查找樹操作主要分為查找，插入和刪除，下面我們來一一介紹。

1.查找

在二叉查找樹中查找一個節點，我們先取根節點，如果它等于我們要查找的數據，那就返回。如果要查找的數據比根節點的值小，那就左子樹中遞歸查找；如果要查找的數據比根節點的值大，那就右子樹中遞歸查找。

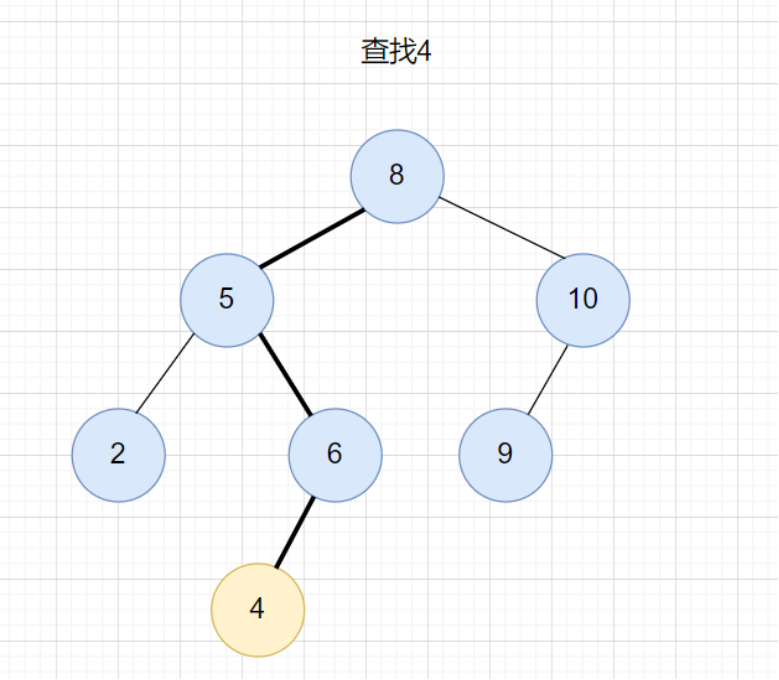
查找的代碼實現:

public class BinarySearchTree {
????private Node root;
????public Node find(int data) {
????????Node temp = root;
????????while (temp != null) {
????????????if (data == temp.data) {
????????????????return temp;
????????????} else if(data > temp.data) {
????????????????temp = temp.rchild;
????????????} else {
????????????????temp = temp.lchild;
????????????}
????????}
????????return null;
????}
}

public class Node {
????int data;
????Node lchild;
????Node rchild;
????public Node(int data) {
????????this.data = data;
????}
}

2.插入

插入的操作類似于查找的操作。從根節點開始，依次比較要插入的數據和節點的關系。 如果要插入的數據比節點的數據大，并且節點的右子樹為空，就將數據直接插入到右子節點的位置，如果右子樹不為空，那就繼續遍歷右子樹；如果要插入的數據比節點的數據小，并且節點的左子樹為空，就將數據直接插入到左子節點的位置，如果左子樹不為空，那就繼續遍歷左子樹。

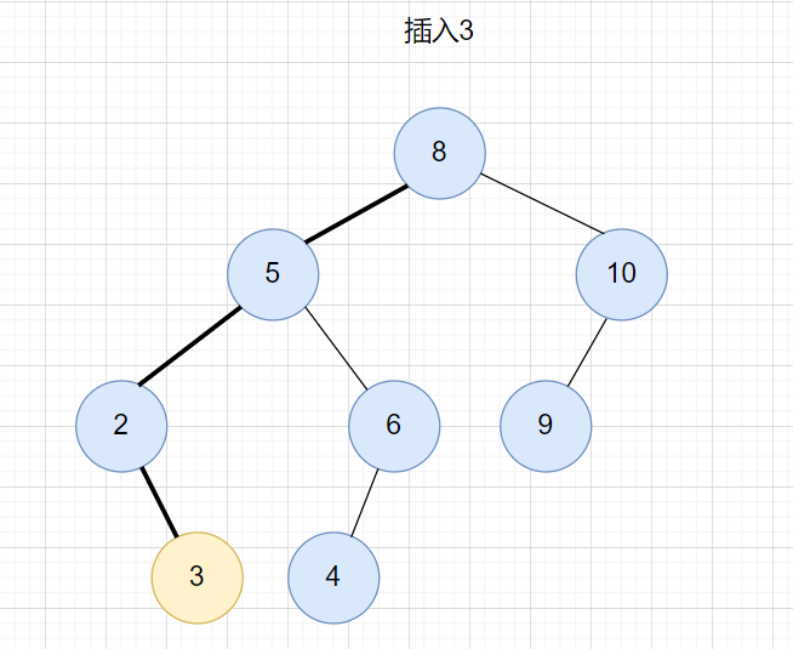
插入的代碼實現:

public void insert(int data) {
????????if (root == null) {
????????????root = new Node(data);
????????????return;
????????}
????????
????????Node temp = root;
????????while (true) {
????????????if (data > temp.data) {
????????????????if (temp.rchild == null) {
????????????????????temp.rchild = new Node(data);
????????????????????return;
????????????????}
????????????????temp = temp.rchild;
????????????} else {
????????????????if (temp.lchild == null) {
????????????????????temp.lchild = new Node(data);
????????????????????return;
????????????????}
????????????????temp = temp.lchild;
????????????}
????????}
}

3.刪除

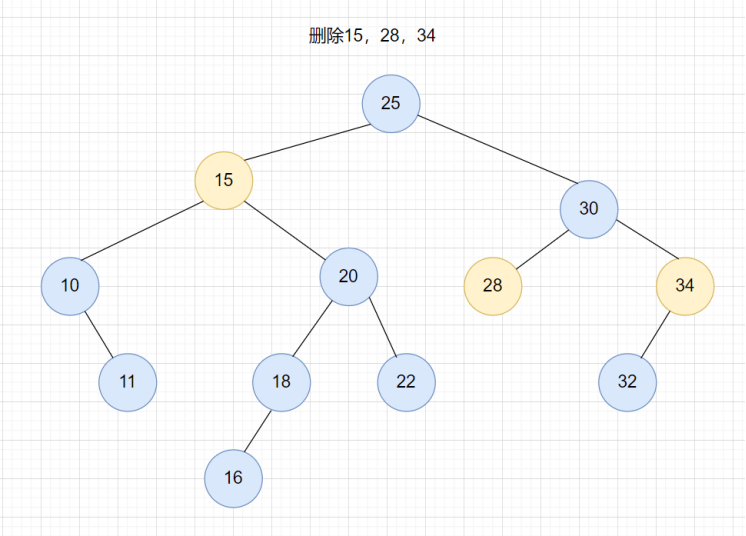
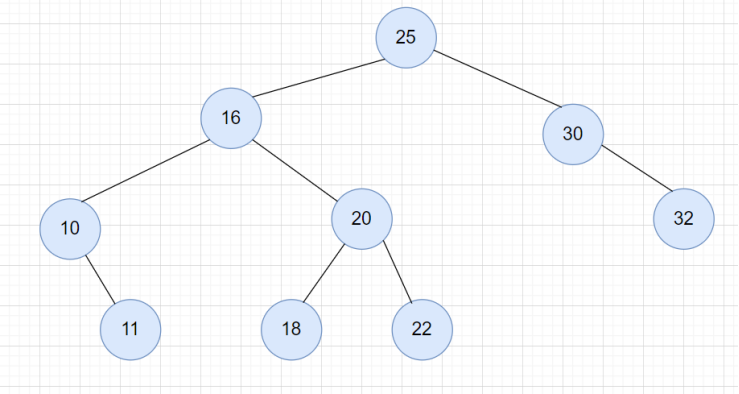
二叉查找樹的查找和插入的操作比較簡單，但是刪除的操作較為復雜，分為三種情況。 第一種情況，要刪除的節點是葉子節點。此時只需要直接將父節點中指向要刪除節點的指針置為null即可。如下圖中刪除28。 第二種情況，要刪除的節點有只有一個子節點（左子節點或右子節點），我們只需要更新父節點中的指針，讓它指向要刪除節點的字節點就可以了。如下圖中的34。 第三種情況，要刪除的節點有兩個子節點。這種情況下，我們需要把要刪除節點的右子樹中最小的節點替換要刪除節點。如下圖中的15。

刪除完成后

代碼實現:

?public void delete(int data) {
????????Node temp = root; ?// temp指向要刪除的節點
????????Node ftemp = null; // ftemp指向要刪除節點的父節點
????????while (temp != null && temp.data != data) {
????????????ftemp = temp;
????????????if (data > temp.data) {
????????????????temp = temp.rchild;
???????????} else {

????????????????temp = temp.lchild;
????????????}
????????}

???????if (temp == null) return; // 沒有找到對應的節點
???????// 若找到，temp就是要刪除的節點
???????// 要刪除的節點有兩個子節點
????????if (temp.lchild != null && temp.rchild != null) {
????????????Node minTemp = temp.rchild; ?// 存儲右子樹的最小節點
????????????Node fminTemp = temp; // minTemp的父節點

????????????// 找到右子樹的最小節點
????????????while (minTemp.lchild != null) {
????????????????fminTemp = minTemp;
????????????????minTemp = minTemp.lchild;
????????????}

????????????temp.data = minTemp.data; // 將最小節點的值替換到temp中
????????????temp = minTemp; ?// 變成刪除葉子節點
????????????ftemp = fminTemp;
????????}

????????// 刪除節點是葉子節點或者僅有一個節點
????????Node child; // temp的子節點
????????if (temp.lchild != null) {
????????????child = temp.lchild;
????????} else if (temp.rchild != null) {
????????????child = temp.rchild;
????????} else {
????????????child = null;
????????}

????????if (ftemp == null) { ?// 刪除的是根節點
???????????root = child;

????????} else if (ftemp.lchild == temp) {
????????????ftemp.lchild = child;
????????} else {
????????????ftemp.rchild = child;
????????}
????}

以上就是對二叉查找樹操作的相關介紹，二叉查找樹本質上是一棵空樹，或者沒有鍵值相等的結點，對二叉查找樹的定義也是相對的。想要深入學習二叉查找樹的小伙伴可以觀看本站的數據結構和算法教程，積累更多關于二叉查找樹的相關知識。