線索二叉樹是指在二叉樹的結點上加上線索的二叉樹。這里的線索指的是對于n個結點的二叉樹，在二叉鏈存儲結構中有n+1個空鏈域，利用這些空鏈域存放在某種遍歷次序下該結點的前驅結點和后繼結點的指針。本文我們就將以這些指針為線索來為大家解析線索二叉樹。

一個二叉樹通過如下的方法“穿起來”：所有原本為空的右孩子指針改為指向該節點在中序序列中的后繼，所有原本為空的左孩子指針改為指向該節點的中序序列的前驅。

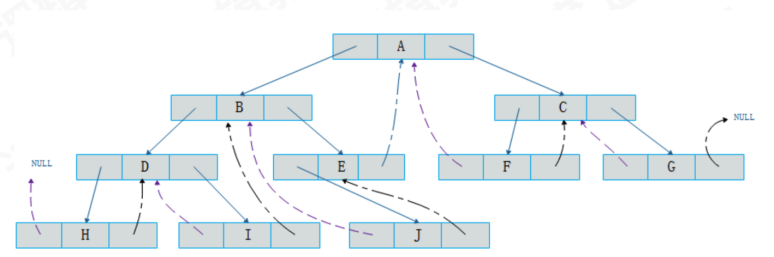
上圖這種加上了線索的二叉鏈表稱為線索鏈表，相應的二叉樹稱為線索二叉樹。

鏈接規則：

1.結點左子樹為空，利用左孩子指針指向它的前驅結點

2.結點右子樹為空，利用右孩子指針指向它的后繼結點

3.注意：所有前驅和后繼只能按照一種遍歷邏輯（例如：中序）

通過考察各種二叉鏈表，不管兒叉樹的形態如何，空鏈域的個數總是多過非空鏈域的個數。準確的說，n各結點的二叉鏈表共有2n個鏈域，非空鏈域為n-1個，但其中的空鏈域卻有n+1個。

根據線索性質的不同，線索二叉樹可分為前序線索二叉樹、中序線索二叉樹和后序線索二叉樹三種。線索鏈表解決了無法直接找到該結點在某種遍歷序列中的前驅和后繼結點的問題，解決了二叉鏈表找左、右孩子困難的問題。

實際上也就是當二叉樹的左右孩子結點為NUll的時候,指向的地址是浪費的,為了減少浪費我們可以通過將其指向前驅或者后續來利用這些無用的空間,提升查找速度,值得注意的是實際使用中我們要根據選擇的二叉樹遍歷規則來進行對應的指向(前序、中序、后序)要保持一直.一般來說我們使用中序遍歷進行二叉樹線索化。

二叉樹的遍歷本質上是將一個復雜的非線性結構轉換為線性結構，使每個結點都有了唯一前驅和后繼（第一個結點無前驅，最后一個結點無后繼）。對于二叉樹的一個結點，查找其左右子女是方便的，其前驅后繼只有在遍歷中得到。為了容易找到前驅和后繼，有兩種方法。一是在結點結構中增加向前和向后的指針，這種方法增加了存儲開銷，不可取；二是利用二叉樹的空鏈指針。

建立線索二叉樹，或者說對二叉樹線索化，實質上就是遍歷一棵二叉樹。在遍歷過程中，訪問結點的操作是檢查當前的左，右指針域是否為空，將它們改為指向前驅結點或后續結點的線索。為實現這一過程，設指針pre始終指向剛剛訪問的結點，即若指針p指向當前結點，則pre指向它的前驅，以便設線索。

二叉樹本身其實就是一種特殊的樹形結構的數據結構，而線索二叉樹又是特殊的二叉樹。所以，線索二叉樹本身的特殊性是值得我們探究的。在本站的數據結構和算法教程中我們也將接觸到更多有意思的數據結構，讓我們在數據結構世界里初窺門徑。