在本文中，我們將討論快速排序算法。快速排序的工作程序也很簡單。

排序是一種以系統方式排列項目的方式。快速排序是廣泛使用的排序算法，它在平均情況下進行n log n比較，以對 n 個元素的數組進行排序。它是一種更快、更高效的排序算法。該算法遵循分而治之的方法。分而治之是一種將算法分解為子問題，然后解決子問題，并將結果組合在一起以解決原始問題的技術。

Divide：在 Divide 中，首先選擇一個樞軸元素。之后，將數組劃分或重新排列為兩個子數組，使得左子數組中的每個元素都小于或等于樞軸元素，而右子數組中的每個元素都大于樞軸元素。

征服：遞歸地，使用快速排序對兩個子數組進行排序。

組合：組合已經排序的數組。

快速排序選擇一個元素作為樞軸，然后圍繞選擇的樞軸元素對給定數組進行分區。在快速排序中，一個大數組被分成兩個數組，其中一個保存小于指定值(樞軸)的值，另一個數組保存大于樞軸的值。

之后，左右子陣列也使用相同的方法進行分區。它將繼續，直到單個元素保留在子數組中。

選擇支點

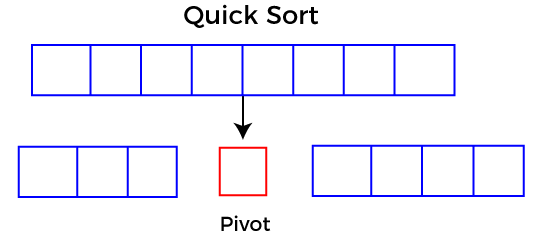
選擇一個好的支點對于快速實現快速排序是必要的。但是，通常確定一個好的支點。選擇支點的一些方法如下 -

樞軸可以是隨機的，即從給定數組中選擇隨機樞軸。

Pivot 可以是給定數組最左邊元素的最右邊元素。

選擇中位數作為樞軸元素。

算法

算法：

QUICKSORT（數組 A，開始，結束）     
{  
如果 （開始 < 結束）      
  {  
  p = 分區（A，開始，結束）  
  QUICKSORT（A，開始，p -  1 ）    
  QUICKSORT (A, p +  1 , 結束)    
  }   
}  

分區算法：

分區算法將子數組重新排列在一個地方。

PARTITION (array A, start, end)     
{  
 pivot ? A[end]     
 i ? start-1     
 for j ? start to end -1 {  
 do if (A[j] < pivot) {    
 then i ? i + 1     
 swap A[i] with A[j]   
  }}   
 swap A[i+1] with A[end]     
 return i+1  
}  

快速排序算法的工作

現在，讓我們看看快速排序算法的工作原理。

為了理解快速排序的工作原理，讓我們看一個未排序的數組。它將使概念更加清晰和易于理解。

讓數組的元素是 

在給定的數組中，我們將最左邊的元素視為樞軸。因此，在這種情況下，a[left] = 24、a[right] = 27 和 a[pivot] = 24。

由于樞軸在左側，因此算法從右側開始并向左移動。

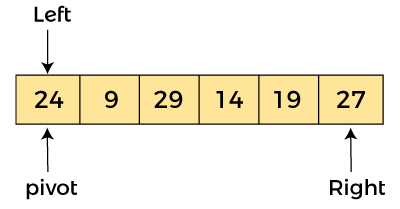
現在，a[pivot] < a[right]，所以算法向左移動一個位置，即 

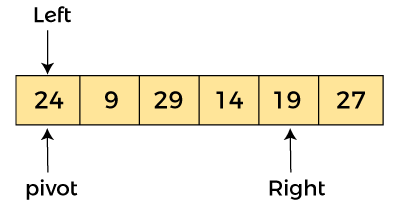
現在，a[left] = 24，a[right] = 19，a[pivot] = 24。

因為，a[pivot] > a[right]，所以，算法將 a[pivot] 與 a[right] 交換，并且樞軸向右移動，如

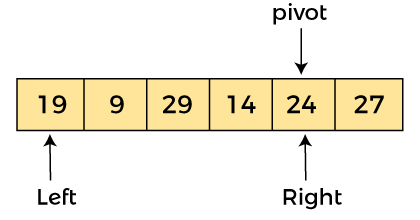
現在，a[left] = 19、a[right] = 24 和 a[pivot] = 24。由于樞軸在右側，所以算法從左開始并向右移動。

由于 a[pivot] > a[left]，所以算法向右移動一個位置 

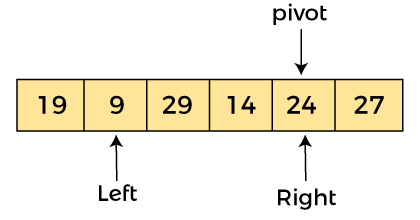
現在，a[left] = 9，a[right] = 24，a[pivot] = 24。由于 a[pivot] > a[left]，所以算法向右移動一個位置 

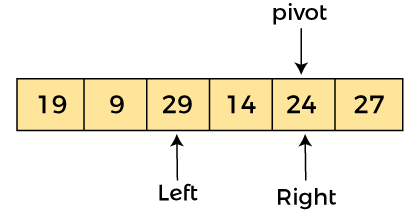
現在，a[left] = 29、a[right] = 24 和 a[pivot] = 24。由于 a[pivot] < a[left]，所以，交換 a[pivot] 和 a[left]，現在進行樞軸在左邊，即

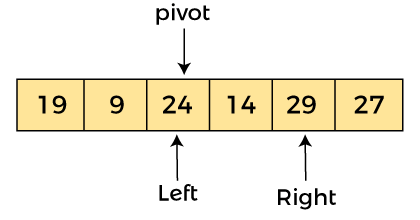
由于樞軸在左側，因此算法從右側開始，然后向左移動。現在，a[left] = 24，a[right] = 29，a[pivot] = 24。由于 a[pivot] < a[right]，所以算法向左移動一個位置，如

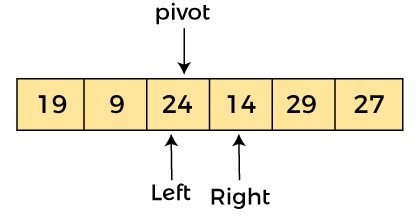
現在，a[pivot] = 24、a[left] = 24 和 a[right] = 14。由于 a[pivot] > a[right]，所以，交換 a[pivot] 和 a[right]，現在進行 pivot在右邊，即

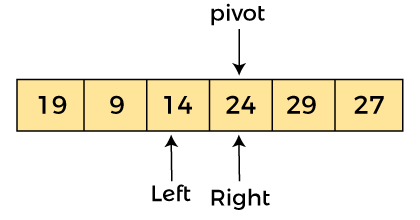
現在，a[pivot] = 24，a[left] = 14，a[right] = 24。pivot 在右邊，所以算法從左開始向右移動。

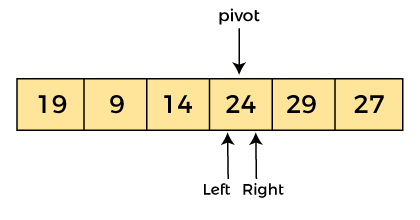
現在，a[pivot] = 24、a[left] = 24 和 a[right] = 24。因此，pivot、left 和 right 指向同一個元素。它代表程序的終止。

作為樞軸元件的元件24被放置在其確切位置。

元素 24 右側的元素大于它，元素 24 左側的元素小于它。

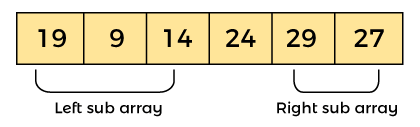
現在，以類似的方式，快速排序算法分別應用于左右子數組。排序完成后，數組將是 

快速排序復雜度

現在，讓我們看看快速排序在最佳情況、平均情況和最壞情況下的時間復雜度。我們還將看到快速排序的空間復雜度。

1.時間復雜度

最佳情況復雜性 -在快速排序中，當樞軸元素是中間元素或靠近中間元素時會出現最佳情況。快速排序的最佳時間復雜度是O(n*logn)。

平均案例復雜度 -當數組元素處于混亂的順序，沒有正確升序和降序時，就會發生這種情況。快速排序的平均案例時間復雜度為O(n*logn)。

最壞情況復雜性 -在快速排序中，當樞軸元素是最大或最小元素時會發生最壞情況。假設，如果樞軸元素始終是數組的最后一個元素，最壞的情況將發生在給定數組已經按升序或降序排序的情況下。快速排序的最壞情況時間復雜度是O(n 2 )。

盡管快速排序的最壞情況復雜度比合并排序和堆排序等其他排序算法要高，但在實踐中它仍然更快。快速排序中最壞的情況很少發生，因為通過更改樞軸的選擇，它可以以不同的方式實現。通過選擇正確的樞軸元素可以避免快速排序中的最壞情況。

2. 空間復雜度

快速排序的空間復雜度為 O(n*logn)。

快速排序的實現

現在，讓我們看看不同編程語言的快速排序程序。

程序：編寫程序以在 Java 中實現快速排序。

公共課 快速   
{  
    /* 將最后一個元素視為樞軸的函數，  
將樞軸放在其確切位置，并放置  
樞軸左側的較小元素和較大的元素  
樞軸右側的元素。*/  
int 分區 ( int  a[],  int  start,  int  end)  
{  
    int  pivot = a[end]; // 樞軸元素  
    int  i = (開始 -  1 );    
    for  ( int  j = start;j <= end -  1 ;j++)  
    {  
        // 如果當前元素小于樞軸  
        如果 (a[j] < 樞軸)  
        {  
            我++； // 增加較小元素的索引  
            int  t = a[i];  
            a[i] = a[j];  
            a[j] = t;  
        }  
    }  
    整數 t = a[i+ 1 ];  
    a[i+ 1 ] = a[結束];  
    a[結束] = t;  
    返回 (i +  1 );  
}    
/* 實現快速排序的函數 */  
void  quick( int  a[],  int  start,  int  end)  /* a[] = 要排序的數組，start = 起始索引，end = 結束索引 */  
{  
    如果 （開始<結束）  
    {  
        int  p = 分區（a，開始，結束）；  //p是分區索引  
        快速（a，開始，p -  1 ）；  
        快速（a，p +  1 ，結束）；  
    }  
}   
/* 打印數組的函數 */  
void  printArr( int  a[],  int  n)  
{  
    詮釋 我;  
    對于 (i =  0 ; i < n; i++)  
        System.out.print(a[i] +  " " );  
}  
    公共靜態無效 主要（字符串[]參數）{    
    int  a[] = {  13 ,  18 ,  27 ,  2 ,  19 ,  25  };  
    int  n = a.length;  
    System.out.println( "\n排序前的數組元素為-" );  
    快速 q1 =  new  Quick();  
    q1.printArr(a, n);  
    q1.quick(a,  0 , n -  1 );  
    System.out.println( "\n排序后的數組元素為-" );  
    q1.printArr(a, n);  
    System.out.println();  
    }  
}  

輸出

執行上述代碼后，輸出將是

以上就是關于“快速排序算法詳解”的介紹，算法還有很多，本站的數據結構和算法教程中找到合適的案例，加強我們對各種排序算法的理解。