1.二叉樹

二叉樹是一種遞歸數據結構，其中每個節點最多可以有 2 個子節點。

二叉樹的一種常見類型是二叉搜索樹，其中每個節點的值都大于或等于左子樹中的節點值，并且小于或等于右子樹中的節點值樹。

這是這種二叉樹的直觀表示：

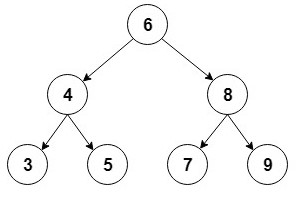
對于實現，我們將使用一個輔助Node類來存儲int值，并保留對每個孩子的引用：

class Node {
    int value;
    Node left;
    Node right;
    Node(int value) {
        this.value = value;
        right = null;
        left = null;
    }
}

然后我們將添加樹的起始節點，通常稱為根：

public class BinaryTree {
    Node root;
    // ...
}

2.常用操作

現在讓我們看看我們可以在二叉樹上執行的最常見的操作。

(1)插入元素

我們要介紹的第一個操作是插入新節點。

首先，我們必須找到要添加新節點的位置，以保持樹的排序。我們將從根節點開始遵循這些規則：

如果新節點的值小于當前節點的值，我們去左子樹

如果新節點的值大于當前節點的值，我們去右子樹

當當前節點為空時，我們到達了一個葉節點，我們可以在該位置插入新節點

然后我們將創建一個遞歸方法來進行插入：

private Node addRecursive(Node current, int value) {
    if (current == null) {
        return new Node(value);
    }
    if (value < current.value) {
        current.left = addRecursive(current.left, value);
    } else if (value > current.value) {
        current.right = addRecursive(current.right, value);
    } else {
        // value already exists
        return current;
    }
    return current;
}

接下來我們將創建從根節點開始遞歸的公共方法：

public void add(int value) {
    root = addRecursive(root, value);
}

讓我們看看如何使用此方法從我們的示例中創建樹：

private BinaryTree createBinaryTree() {
    BinaryTree bt = new BinaryTree();
    bt.add(6);
    bt.add(4);
    bt.add(8);
    bt.add(3);
    bt.add(5);
    bt.add(7);
    bt.add(9);
    return bt;
}

(2)尋找元素

現在讓我們添加一個方法來檢查樹是否包含特定值。

和以前一樣，我們將首先創建一個遍歷樹的遞歸方法：

private boolean containsNodeRecursive(Node current, int value) {
    if (current == null) {
        return false;
    } 
    if (value == current.value) {
        return true;
    } 
    return value < current.value
      ? containsNodeRecursive(current.left, value)
      : containsNodeRecursive(current.right, value);
}

在這里，我們通過將其與當前節點中的值進行比較來搜索該值;然后，我們將根據結果繼續左或右孩子。

接下來，我們將創建從root開始的公共方法：

public boolean containsNode(int value) {
    return containsNodeRecursive(root, value);
}

然后我們將創建一個簡單的測試來驗證樹是否真的包含插入的元素：

@Test
public void givenABinaryTree_WhenAddingElements_ThenTreeContainsThoseElements() {
    BinaryTree bt = createBinaryTree();
    assertTrue(bt.containsNode(6));
    assertTrue(bt.containsNode(4)); 
    assertFalse(bt.containsNode(1));
}

添加的所有節點都應包含在樹中。

(3)刪除元素

另一種常見的操作是從樹中刪除一個節點。

首先，我們必須以與之前類似的方式找到要刪除的節點：

private Node deleteRecursive(Node current, int value) {
    if (current == null) {
        return null;
    }
    if (value == current.value) {
        // Node to delete found
        // ... code to delete the node will go here
    } 
    if (value < current.value) {
        current.left = deleteRecursive(current.left, value);
        return current;
    }
    current.right = deleteRecursive(current.right, value);
    return current;
}

一旦我們找到要刪除的節點，主要有 3 種不同的情況：

一個節點沒有孩子——這是最簡單的情況;我們只需要在它的父節點中用null替換這個節點

一個節點只有一個孩子——在父節點中，我們用它唯一的孩子替換這個節點。

一個節點有兩個孩子——這是最復雜的情??況，因為它需要樹重組

讓我們看看當節點是葉節點時如何實現第一種情況：

if (current.left == null && current.right == null) {
    return null;
}

現在讓我們繼續討論節點有一個孩子的情況：

if (current.right == null) {
    return current.left;
}
if (current.left == null) {
    return current.right;
}

在這里，我們返回非空子節點，以便將其分配給父節點。

最后，我們必須處理節點有兩個孩子的情況。

首先，我們需要找到將替換已刪除節點的節點。我們將使用即將被刪除節點的右子樹的最小節點：

private int findSmallestValue(Node root) {
    return root.left == null ? root.value : findSmallestValue(root.left);
}

然后我們將最小值分配給要刪除的節點，然后，我們將從右子樹中刪除它：

int smallestValue = findSmallestValue(current.right);
current.value = smallestValue;
current.right = deleteRecursive(current.right, smallestValue);
return current;

最后，我們將創建從根開始刪除的公共方法：

public void delete(int value) {
    root = deleteRecursive(root, value);
}

現在讓我們檢查刪除是否按預期工作：

@Test
public void givenABinaryTree_WhenDeletingElements_ThenTreeDoesNotContainThoseElements() {
    BinaryTree bt = createBinaryTree();
    assertTrue(bt.containsNode(9));
    bt.delete(9);
    assertFalse(bt.containsNode(9));
}