對(duì)于計(jì)算機(jī)科學(xué)來說，算法至關(guān)重要。通俗地講，算法是指解決問題的一種方法或者一個(gè)過程。嚴(yán)格來講，算法是由若干條指令組成的有序序列，且滿足以下4條性質(zhì)：

    1.輸入

    2.輸出

    3.確定性

    4.有限性

    算法復(fù)雜度的高低體現(xiàn)在運(yùn)行該算法時(shí)所需要的計(jì)算機(jī)資源的多少上，所需資源越多，算法的復(fù)雜度越高，也就稱這個(gè)算法較差。因此，算法的復(fù)雜度分為時(shí)間復(fù)雜度和空間復(fù)雜度。

    由于空間復(fù)雜度是具體算法具體分析，因此這里我們簡(jiǎn)單談一談時(shí)間復(fù)雜度。

    普通函數(shù)的時(shí)間復(fù)雜度大致分為4個(gè)步驟：確定循環(huán)條件->確定循環(huán)變量的變化規(guī)律->假設(shè)執(zhí)行了i次->計(jì)算i并帶回原方程。

    遵循了上述四個(gè)步驟就能求解大部分的算法時(shí)間復(fù)雜度了。

    對(duì)于遞歸函數(shù)，我們舉一個(gè)簡(jiǎn)單的例子來說明。

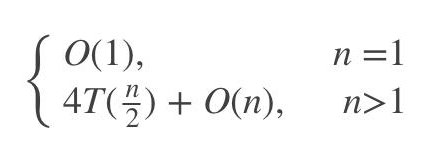
    這是一個(gè)求解大整數(shù)乘法的遞歸表達(dá)式，對(duì)于它的時(shí)間復(fù)雜度，其計(jì)算過程如下：

    T(n)=4T(n/2)+O(n)

    =4[4T(n/4)+O(n/2)]+O(n)=4^2T(n/4)+3O(n)

    =4^2[4T(n/8)+O(n/4)]+3O(n)=4^3T(n/8)+7O(n)

    ......

    =4^xT(n/2^x)+(2^x-1)O(n)//假設(shè)執(zhí)行了x次

    令n=2^x帶入上面方程T(n)=n^2+(n-1)n

    因此時(shí)間復(fù)雜度為O(n^2)

    再看下面這個(gè)

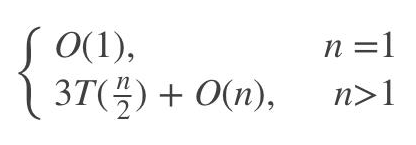
    這是對(duì)大整數(shù)乘法的另一種優(yōu)化算法，具體思想我就不再這里贅述了

    對(duì)于這個(gè)表達(dá)式，我們還是按照上面的方法一步一步的來

    T(n)=3T(n/2)+O(n)

    =3[3T(n/4)+O(n/2)]+O(n)=3^2T(n/4)+(3/2+1)O(n)

    =3^2[3T(n/8)+O(n/4)]+(3/2+1)O(n)=3^3T(n/8)+(3^2/2^2+3/2+1)O(n)

    ……

    =3^xT(n/2^x)+(3^x-1/2^x-1+3^x-2/2^x-2+......+3^2/2^2+3/2+1)O(n)

    易知后面括號(hào)里其實(shí)是首項(xiàng)為1，公比為3/2的等比數(shù)列的前n-1項(xiàng)和

    因此上式

    =3^xT(n/2^x)+[4(3^x-1/2^x)-2]O(n)

    令n=2^x，則x=log2(n),帶入

    =3^log2(n)+{4[(3^log2(n/2))/n]-2}O(n)

    =n^log2(3)+4/3(n^log2(3))-2n

    =5/3n^log2(3)-2n

    u因此時(shí)間復(fù)雜度為O(n^log2(3))=O(n^1.59)

    因?yàn)镺(n^1.59)

    所以后面這種算法是優(yōu)于前面那一種算法的。

    你看，都是解決大整數(shù)乘法的問題，通過不同的算法，我們求解問題所花的時(shí)間也不同，所以，在計(jì)算機(jī)的發(fā)展中，尋找最優(yōu)算法是一直在路上的。

　以上就是動(dòng)力節(jié)點(diǎn)java培訓(xùn)機(jī)構(gòu)的小編針對(duì)“Java基礎(chǔ)學(xué)習(xí)：java遞歸函數(shù)例子”的內(nèi)容進(jìn)行的回答，希望對(duì)大家有所幫助，如有疑問，請(qǐng)?jiān)诰€咨詢，有專業(yè)老師隨時(shí)為你服務(wù)。