更新時間:2020-02-25 12:26:47 來源:動力節點 瀏覽2415次
如果一個數組在排序之后,每相鄰兩個數差的絕對值都為1,則該數組為可整合數組。例如:[5,3,4,6,2]排序之后為[2,3,4,5,6],符合每相鄰兩個數差的絕對值都為1,所以這個數組為可整合數組。

給定一個整型數組arr,要求返回其中最大可整合數組的長度。例如,[5,5,3,2,6,4,3]的最大整合子數組為[5,3,2,6,4],所以返回5.
時間復雜度高但容易理解的做法。對arr中的每一個子數組arr[i……j](0<=i<=j<=N-1),都驗證一下是否符合可整合數組的定義,也就是把arr[i……j]排序一下,看是否依次遞增且每次遞增1.然后在所有符合整合數組定義的子數組中,記錄最大的那個長度,返回即可。需要注意的是,在考查每一個arr[i……j]是否符合可整合數組定義的時候,都得把arr[i……j]單獨復制成一個新的數組,然后把這個新的數組排序、驗證,而不能直接改變arr中元素的順序。大體過程如下:依次考查每一個子數組arr[i……j](0<=i<=j<=N-1),一共有O(N^2)個。2.對每一個子數組arr[i……j],復制成一個新的數組,記為newArr,把newArr排序,然后驗證是否符合可整合數組的定義,這一步代價為O(NlogN)。3.步驟2中符合條件的、最大的那個子數組的長度就是結果。
具體過程看如下代碼中的getLIL1方法,時間復雜度為O(N^2)*O(NlogN)-O(N^3logN).

第一種方法嚴格按照定義來驗證每一個子數組是否是可整合數組,但是驗證可整合數組真的需要如此麻煩嗎?有沒有更好的方法來加速驗證過程?這也是下面要提供方法的核心。判斷一個數組是否是可整合數組還可以用以下方法來判斷,一個數組中如果沒有重復元素,并且如果最大值減去最小值,再加1的結果等于元素個數(max-min+1==元素個數),那么這個數組就是可整合數組。比如[3,2,5,6,4],max-min+1=6-2+1=5==元素個數,所以這個數組是可整合數組。這樣,驗證每一個子數組是否是可整合數組的時間復雜度可以從第一種方法的O(NlogN)加速至O(1),整個過程的時間復雜度就可加速到O(N^2),具體請參看如下代碼中的getLIL2方法。
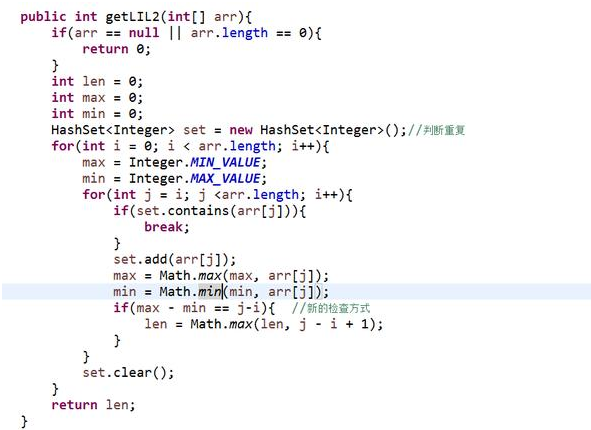
算法與數據結構--最長的可整合子數組的長度的普通解法和進階解法(java實現)
以上就是動力節點Java培訓機構小編介紹的“Java培訓教程:Java數組長度的普通解法和進階解法”的內容,希望對大家有幫助,如有疑問,請在線咨詢,有專業老師隨時為你服務。
 Java實驗班
Java實驗班
0基礎 0學費 15天面授
 Java就業班
Java就業班
有基礎 直達就業
 Java夜校直播班
Java夜校直播班
業余時間 高薪轉行
 Java在職加薪班
Java在職加薪班
工作1~3年,加薪神器
 Java架構師班
Java架構師班
工作3~5年,晉升架構
提交申請后,顧問老師會電話與您溝通安排學習

